Simple Curve Fitting with the Gauss-Newton Algorithm

$\newcommand{\mvec}[1]{\mathbf{#1}}\newcommand{\gvec}[1]{\boldsymbol{#1}}\definecolor{eqcol2}{RGB}{114,0,172}\definecolor{eqcol1}{RGB}{172,0,114}\definecolor{eqcol3}{RGB}{0,172,114}\definecolor{eqcol4}{RGB}{230,190,120}$In the description of the physically based rendering implementation of Unreal Engine 4[1], Karis states that instead of using the classical Fresnel formula \begin{align*} F(\mvec{v},\mvec{h}) = F_0 + (1-F_0)(1 - \mvec{v}\cdot\mvec{h})^5 \end{align*} he is using the approximation \begin{align*} F(\mvec{v},\mvec{h}) = F_0 + (1-F_0)2^{ (−5.55473(\mvec{v}\cdot\mvec{h}) −6.98316)(\mvec{v}\cdot\mvec{h}) } \end{align*} Note that $-5.55473$ and $−6.98316$ are oddly exact numbers. It is unkely that Karis found them by guessing. Instead, it is more likely that they were found by some numerical algorithm. In this article, we shall describe one method that could have been used for finding these constants.

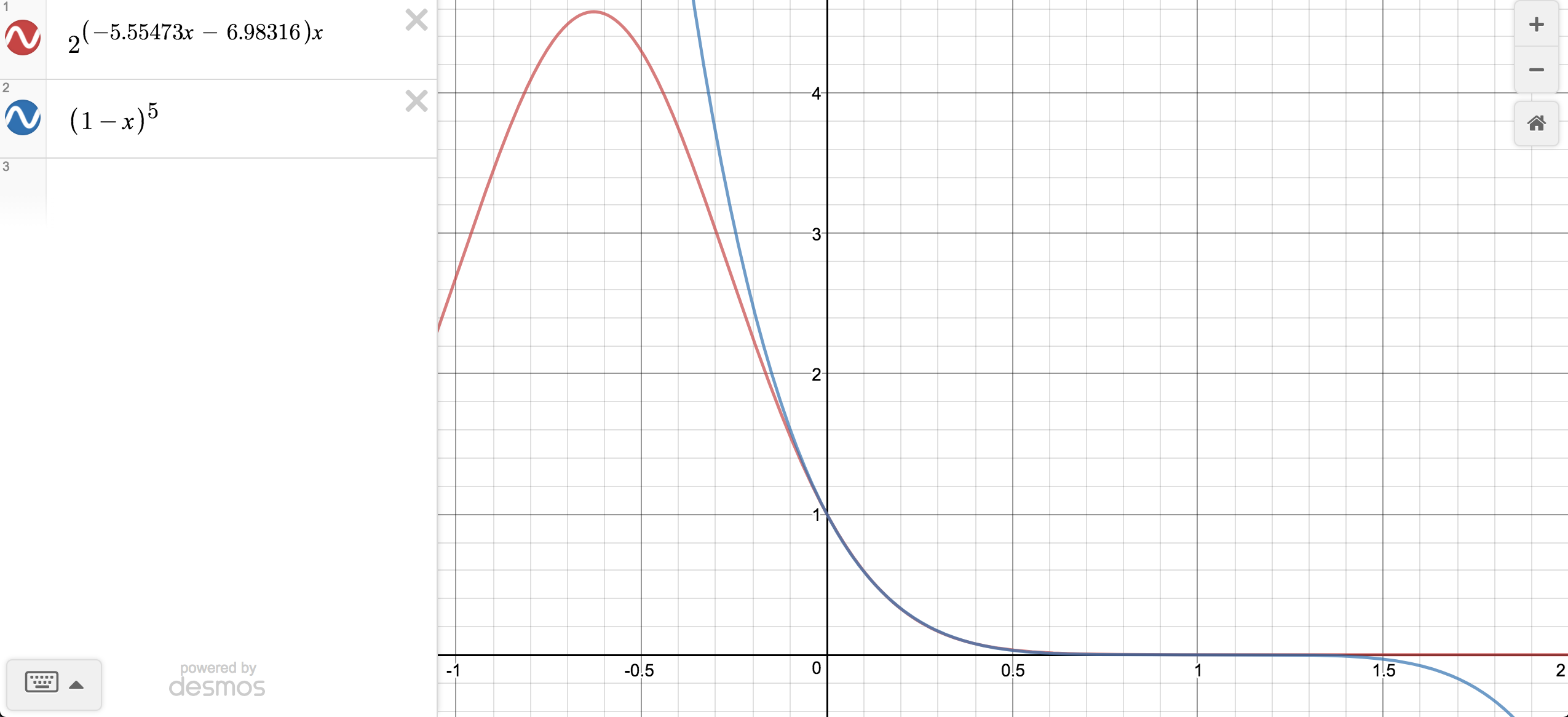
First, note that $\mvec{v}$ and $\mvec{h}$ are in practice always normalized before they are used in the Fresnel formula. But then we must have $0 \le \mvec{v}\cdot\mvec{h} \le 1$, by the definition of the dot product. Consequently, if we want to find an approximation for $(1 - \mvec{v}\cdot\mvec{h})^5$, it is sufficient to find an approximation for $(1 - x)^5$, where $0 \le x \le 1$, since this is the only interval that is of interest when we are using the Fresnel formula. Within this interval, Karis finds the approximation $2^{ (−5.55473x −6.98316)x}$. Indeed, plotting reveals that this approximation is only useful within the interval $0 \le x \le 1$:

We shall denote this interval $0 \le x \le 1$ the domain of our curve fitting problem.

We shall use the root mean square error(RMSE) to measure the quality of an approximation. The root mean square error between some original function $y(x)$ and its approximation $\hat{y}(x)$ is given by \begin{align*} RMSE = \sqrt{ \frac{\sum_{i=1}^N (y(x_i) - \hat{y}(x_i))^2}{n}}. \end{align*} That is, we define $N$ sample points at which we evaluate $y$ and $\hat{y}$. These sample points are uniformly distributed on the domain. For instance, if $N=5$, then the sample points are $x_1=0.00$, $x_2=0.25$, $x_3=0.50$, $x_4=0.75$, $x_5=1.00$. At every such sample point, we evaluate the squared difference between the original function and the approximation: $(y(x_i) - \hat{y}(x_i))^2$. If all these squared differences were 0, then $\hat{y}$ would be a very close fit to $y$, assuming that the number of sample points $N$ is large. The higher $N$ is, the better we can measure the similarity of $y$ and $\hat{y}$.

Finally, the sum of the squared differences is divided by the number of samples $N$ and then the square root is taken, and the result of this is the RMSE. These last two steps are done for the purpose of normalization.

The approximation of Karis has a RMSE of $0.002238$ with respect to the original Fresnel function $(1-x)^5$. For properly chosen values of $A$ and $B$, the curve of $2^{(Ax + B)x}$ is close to $(1-x)^5$. For instance, the assignments $A=-5$ and $B=-7$ result in an RMSE of $0.003689$. However, this is clearly worse than the approximation of Karis, where $A=-5.55473$ and $B=−6.98316$. What is necessary is an algorithm that allows us to find values of these two parameters that result in a low RMSE. One such algorithm shall described in the following section.

The Gauss-Newton Algorithm

As a simple example, let us say we have a function $y(x)$ we want to approximate by some approximation $\hat{y}(x,p)$. Here $p$ is the parameter of the approximation. $\hat{y}$ could be $px^2$ or $px$ for instance, and we require a value of $p$ that result in $\hat{y}$ having a low RMSE. We start with an initial guess for $p$, and then update $p$ by adding some update step $h$ to it. Ideally, adding $h$ to $p$ should make our approximation move closer to $y$. Now, the main issue is determining a good value for $h$. As a first step, we approximate the value of $\hat{y}(x,p+h)$ by a first order taylor series at $p$ \begin{align*} \hat{y}(x,p+h) \approx \hat{y}(x,p) + (p+h-p)\frac{\partial \hat{y}}{\partial p}(x,p) = \hat{y}(x,p) + h\frac{\partial \hat{y}}{\partial p}(x,p) \end{align*} Define $S$ as the sum of the squared differences between $y$ and $\hat{y}$ \begin{align*} S = \sum_{i=1}^N (y(x_i) - \hat{y}(x_i,p))^2 \end{align*} If $S$ is small, then $\hat{y}$ is a good approximation(we are using $S$ instead of RMSE, since it is easier to deal with algebraically). Our chief objective is to find a value of $h$ that moves $\hat{y}$ closer to $y$. To achieve this, we substitute our Taylor approximation for $\hat{y}(h,p+h)$ into the expression for $S$ \begin{align*} S = \sum_{i=1}^N (y(x_i) - (\hat{y}(x_i,p) + h\frac{\partial \hat{y}}{\partial p}(x_i,p)))^2 = \sum_{i=1}^N (y(x_i) - \hat{y}(x_i,p) - h\frac{\partial \hat{y}}{\partial p}(x_i,p))^2 \end{align*} We will find a value for $h$ that minimizes $S$, and this will be our update step. For this purpose, the partial derivative of $S$ with respect to $h$ is calculated \begin{align*} \frac{\partial S}{\partial h} = -2\sum_{i=1}^N \left[ \left(y(x_i) - \hat{y}(x_i,p) - h\frac{\partial \hat{y}}{\partial p}(x_i,p)\right)\frac{\partial \hat{y}}{\partial p}(x_i,p) \right] \end{align*} the value of $h$ for which $\frac{\partial S}{\partial h} = 0$, is either a local minimum or maximum, or a saddle point, depending on the sign of the second derivative: \begin{align*} \frac{\partial^2 S}{\partial h^2} = +2\sum_{i=1}^N \left[ \left(\frac{\partial \hat{y}}{\partial p}(x_i,p)\right)^2 \right] \end{align*} So we clearly have $\frac{\partial^2 S}{\partial h^2} \ge 0$, since a squared number must be positive(since we are not dealing with any complex numbers here!). If $\frac{\partial^2 S}{\partial h^2} > 0$ for some value of $h$, then for sure that value of $h$ is a good value for our purposes, as this value of $h$ is at a local minimum. However, it could occur that the value of $\left(\frac{\partial \hat{y}}{\partial p}(x_i,p)\right)^2$ is zero at all sample points, and then $\frac{\partial^2 S}{\partial h^2} = 0$, meaning that $h$ is at a saddle point, and not a local minimum. However, this is a very unlikely event, and we found that even if we ignored this possibility, good results were obtained in the end.

Therefore, to find a good value for $h$, we set the first partial derivative to zero and solve for $h$, in order to find the value of $h$ for which we have a local minimum: \begin{align*} -2\sum_{i=1}^N \left[ \left(y(x_i) - \hat{y}(x_i,p) - h\frac{\partial \hat{y}}{\partial p}(x_i,p)\right)\frac{\partial \hat{y}}{\partial p}(x_i,p) \right] = 0 \\ \end{align*} Rearranging the above yields \begin{equation} \left( \sum_{i=1}^N \left(\frac{\partial \hat{y}}{\partial p}(x_i,p) \right)^2 \right)h = \sum_{i=1}^N \left( \left( y(x_i) - \hat{y}(x_i,p) \right) \frac{\partial \hat{y}}{\partial p}(x_i,p) \right) \label{eq:single} \end{equation} Therefore, to compute a value of $h$ that will move $\hat{y}(x,p)$ closer to $y(x)$, we simply solve for $h$ in equation $\eqref{eq:single}$. The new value of $p$ shall be set to $p+h$. Then $h$ will be solved for again, and $p$ will be updated again, and this iterative scheme is repeated until the RMSE is small enough. This algorithm is called the Gauss-Newton Algorithm.

In practice, $\hat{y}$ will often be dependent on several $m$ parameters and not a single parameter, so that $p$ is instead a vector $\mvec{p}$ of dimensions $m \times 1$, so that our approximation is instead written $\hat{y}(x, \mvec{p})$. The update step is also a vector $\mvec{h}$ of dimensions $m \times 1$. For every iteration, we will find our update step by solving the matrix equation \begin{equation} [\mvec{J}^T \mvec{J}] \mvec{h} = \mvec{J}^T (\mvec{y} - \mvec{\hat{y}}) \label{eq:multi} \end{equation} The jacobian matrix $\mvec{J}$ is a matrix with dimensions $n \times m$. It is defined as follows: In column $j$ in row $i$, we store the value $\frac{\partial \hat{y}}{\partial p_j}(x_i, \mvec{p})$. So the jacobian simply stores the values of the partial derivatives for all the sample points. Finally, the vectors $\mvec{y}$ and $\mvec{\hat{y}}$ contains the values of $y(x)$ and $\hat{y}(x,\mvec{p})$ evaluated at all the sample points. Finally, note that $\eqref{eq:multi}$ is simply a generalization of $\eqref{eq:single}$. The derivation of this more general equation is slightly more involved, since it involves matrices and vectors, but the derivation is still based on the exact same principles that we applied when deriving equation $\eqref{eq:single}$. The interested reader may peruse section 3 in [2] for a derivation of $\eqref{eq:multi}$.

Gauss-Newton for Curve Fitting

With the Gauss-Newton algorithm in our hands, we can focus our attention on the initial problem: finding values of the parameters $A$ and $B$ such that $2^{(Ax + B)x}$ approximates $(1-x)^5$ with a small RMSE. We denote this approximation $\hat{y}(x,A,B) = 2^{(Ax + B)x}$. In order to utilize the Gauss-Newton algorithm, the partial derivatives must be found: \begin{align*} \frac{\partial\hat{y}}{\partial A}(x,A,B) &= x^2\ln(2) \cdot 2^{(Ax + B)x}\\ \frac{\partial\hat{y}}{\partial B}(x,A,B) &= x\ln(2) \cdot 2^{(Ax + B)x} \end{align*} These two partial derivatives are used to form the linear system $\eqref{eq:multi}$. Once this system has been formed, it can be solved by using Eigen. By solving the system, the update step $\mvec{h}$ is obtained, and this value is added to $A$ and $B$ to improve the RMSE. By running the Gauss-Newton algorithm for a number of iterations, it is found that the parameter values $A=-5.55473$ and $B=6.98316$(these values are rounded) minimize the RSME. These are also exactly the values that Karis used, and now we finally know how Karis obtained those two values in the first place: probably by using the Gauss-Newton algorithm, or some similar algorithm.

Source code that implements the Gauss-Newton algorithm to find the parameters $A=-5.55473$ and $B=6.98316$ can be found in a gist.

References

[1] Brian Karis, "Real Shading in Unreal Engine 4". Link.

[2] Henri P. Gavin, "The Levenberg-Marquardt method for nonlinear least squares curve-fitting problems". Link.